读《Transformer》

节选了部分原论文内容，认真读一下这篇大名鼎鼎的transformer，旨在加深理解和学英语O(∩_∩)O

Attention Is All You Need

有点霸气

abstract

The dominant sequence transduction models are based on complex recurrent or convolutional neural networks that include an encoder and a decoder.

主流的序列转换模型都是基于包含编码器和解码器的循环或卷积神经网络。

The best performing models also connect the encoder and decoder through an attention mechanism.

表现最好的模型也是通过注意力机制连接编码器和解码器。

We propose a new simple network architecture, the Transformer, based solely on attention mechanisms, dispensing with recurrence and convolutions entirely.

我们提出了一种新型简单的网络架构，Transformer，只基于注意力机制，完全不需要循环和卷积。

Experiments on two machine translation tasks show these models to be superior in quality while being more parallelizable and requiring significantly less time to train.

在两个机器翻译任务的实验上表现出这些模型具有更好的质量，同时具有更强的并行性，训练时间明显减少。

Our model achieves 28.4 BLEU on the WMT 2014 English-to-German translation task, improving over the existing best results, including ensembles, by over 2 BLEU. On the WMT 2014 English-to-French translation task, our model establishes a new single-model state-of-the-art BLEU score of 41.8 after training for 3.5 days on eight GPUs, a small fraction of the training costs of the best models from the literature.

我们的模型在WMT2014英转德翻译任务上实现了28.4 BLEU，比目前全部最好的结果提高了2 BLEU。在WMT2014英转法翻译任务上，我们的模型在 8个GPU训练了3天半（文献中最好模型训练成本的一小部分）后以41.8刷新了单模型最高的BLUE成绩。

We show that the Transformer generalizes well to other tasks by applying it successfully to English constituency parsing both with large and limited training data.

把它成功用在大量和有限的训练数据的英语语句成分分析表明了Transformer在其他任务上具有不错的泛化性。

1.Introduction

Recurrent neural networks, long short-term memory and gated recurrent neural networks in particular, have been firmly established as state of the art approaches in sequence modeling and transduction problems such as language modeling and machine translation. Numerous efforts have since continued to push the boundaries of recurrent language models and encoder-decoder architectures.

RNN，特别是LSTM和门控RNN，已经在像语言模型化和机器翻译这样的序列模型化和转换问题被坚定地确立为最先进的方法。此后许多努力继续推动循环语言模型和编解码架构的边界。

Recurrent models typically factor computation along the symbol positions of the input and output sequences. Aligning the positions to steps in computation time, they generate a sequence of hidden states $h_t$ , as a function of the previous hidden state $h_{t-1}$ and the input for position $t$ .

循环模型通常考虑沿着输入和输出序列的符号位置计算。把位置和计算时间的步数对齐，他们产生一个隐藏状态序列 $h_t$ ，作为先前的隐藏状态 $h_{t-1}$ 和位置 $t$ 输入的函数。

This inherently sequential nature precludes parallelization within training examples, which becomes critical at longer sequence lengths, as memory constraints limit batching across examples.Recent work has achieved significant improvements in computational efficiency through factorization tricks and conditional computation, while also improving model performance in case of the latter. The fundamental constraint of sequential computation, however, remains.

这种固有的顺序性排除了在训练样本时并行化，对于较长的序列变得严重因为内存约束限制样本批处理。最近的工作通过分解技巧和条件计算已经显著改善了计算效率，同时后者也提高了模型性能。然而序列计算的基本限制仍然存在。

Attention mechanisms have become an integral part of compelling sequence modeling and transduction models in various tasks, allowing modeling of dependencies without regard to their distance in the input or output sequences. In all but a few cases, however, such attention mechanisms are used in conjunction with a recurrent network.

注意力机制已经成为在许多任务中引人注目的序列模型和转换模型不可或缺的一部分，允许对依赖关系进行建模，而不考虑它们在输入或输出序列中的距离。然而除了少数外，这种注意力机制被用在与循环网络结合。

In this work we propose the Transformer, a model architecture eschewing recurrence and instead relying entirely on an attention mechanism to draw global dependencies between input and output. The Transformer allows for significantly more parallelization and can reach a new state of the art in translation quality after being trained for as little as twelve hours on eight P100 GPUs.

这次我们提出了Transformer，一种避免循环也不完全依赖注意力机制来描述输入输出间的全局依赖关系的模型架构。Transformer明显允许更强的并行化并且能够在8个P100 GPU上被训练仅12个小时后达到翻译质量的一个新境界。

2.Background

The goal of reducing sequential computation also forms the foundation of the Extended Neural GPU, ByteNet and ConvS2S, all of which use convolutional neural networks as basic building block, computing hidden representations in parallel for all input and output positions. In these models, the number of operations required to relate signals from two arbitrary input or output positions grows in the distance between positions, linearly for ConvS2S and logarithmically for ByteNet. This makes it more difficult to learn dependencies between distant positions. In the Transformer this is reduced to a constant number of operations, albeit at the cost of reduced effective resolution due to averaging attention-weighted positions, an effect we counteract with Multi-Head Attention as described in section 3.2.

减少顺序计算的目标也形成了Extended Neural GPU，ByteNet和ConvS2S的基础，他们都使用卷积神经网络作为基础构建块，对所有的输入输出位置并行计算隐藏层。在这些模型中，将任意两个输入或输出位置信号关联起来的参数随着两个位置的距离增长，ConS2S是线性的，ByteNet是对数的。这使得远距离位置的依赖关系难以学习。在Transformer中尽管由于平均注意力加权位置减少有效分辨率为代价，这被简化成一个常量，我们用在3.2节描述的多头注意力来抵消这个效果。

Self-attention, sometimes called intra-attention is an attention mechanism relating different positions of a single sequence in order to compute a representation of the sequence. Self-attention has been used successfully in a variety of tasks including reading comprehension, abstractive summarization, textual entailment and learning task-independent sentence representations.

自注意力，有时被称为内注意力，是一种关于一个信号序列的不同位置的注意力机制，为了计算这个序列的表征。自注意力已经被成功地用在各种各样的任务中包括阅读理解，抽象概括，文本语义和依赖于语句特征的学习任务。

End-to-end memory networks are based on a recurrent attention mechanism instead of sequence aligned recurrence and have been shown to perform well on simple-language question answering and language modeling tasks.

端到端记忆网络基于循环注意力机制而不是序列对齐的循环并且已被证明在简单语言问答和语言建模任务上表现很好。

To the best of our knowledge, however, the Transformer is the first transduction model relying entirely on self-attention to compute representations of its input and output without using sequence-aligned RNNs or convolution.

然而，据我们所知，Transformer是第一个没有使用序列对齐的RNN或者卷积完全依赖自注意力来计算输入输出的特征的转换模型。

3.Model Architecture

Most competitive neural sequence transduction models have an encoder-decoder structure. Here, the encoder maps an input sequence of symbol representations ($x_1,...,x_n$) to a sequence of continuous representations $z=(z_1,...,z_n)$ Given $z$ , the decoder then generates an output sequence $(y_1,...,y_m)$ of symbols one element at a time. At each step the model is auto-regressive, consuming the previously generated symbols as additional input when generating the next.

大多具有竞争力的神经序列转换模型用编解码的架构。这里，编码器映射由($x_1,...,x_n$)表示的输入序列到由 $z=(z_1,...,z_n)$ 表示的连续序列，然后解码器一次生成一个由$(y_1,...,y_m)$表示的输出序列中的一个元素。每一步模型是自动回归的，当生成下一个时用先前生成的特征作为加性输入。

The Transformer follows this overall architecture using stacked self-attention and point-wise, fully connected layers for both the encoder and decoder, shown in the left and right halves of Figure 1, respectively.

Transformer遵循使用自注意力堆叠和整体架构和逐点全连接层的编码器和解码器的整体架构，分别展示在Figue 1的左右两部分。

3.1Encoder and Decoder Stacks

Encoder: The encoder is composed of a stack of $N = 6$ identical layers. Each layer has two sub-layers. The first is a multi-head self-attention mechanism, and the second is a simple, position-wise fully connected feed-forward network. We employ a residual connection around each of the two sub-layers, followed by layer normalization. That is, the output of each sub-layer is $LayerNorm(x + Sublayer(x))$ , where $Sublayer(x)$ is the function implemented by the sub-layer itself. To facilitate these residual connections, all sub-layers in the model, as well as the embedding layers, produce outputs of dimension $d_{model} = 512$ .

编码器：编码器由$N = 6$完全一样的层的栈构成的。每一层有两个子层。第一层是多头自注意力机制，第二层是一个简单的按位置全连接的前馈网络。我们在两个子层的每一层周围用了残差连接，接着层归一化。也就是说，每一个子层的输出是$LayerNorm(x + Sublayer(x))$，这里的$Sublayer(x)$是子层本身实现的函数。为了方便这些残差连接，所有模型的子层还有嵌入层的输出维度是$d_{model} = 512$。

Decoder: The decoder is also composed of a stack of $N = 6$ identical layers. In addition to the two sub-layers in each encoder layer, the decoder inserts a third sub-layer, which performs multi-head attention over the output of the encoder stack. Similar to the encoder, we employ residual connections around each of the sub-layers, followed by layer normalization. We also modify the self-attention sub-layer in the decoder stack to prevent positions from attending to subsequent positions. This masking, combined with fact that the output embeddings are offset by one position, ensures that the predictions for position $i$ can depend only on the known outputs at positions less than $i$.

解码器：解码器也是由$N = 6$完全一样的层的栈构成的。除了在每个编码器层的两个子层，解码器插入了第三个子层，他对编码器栈的输出做多头注意力。跟编码器相似，我们也在每个子层周围用残差连接，接着层归一化。我们也修改了解码器栈的自注意子层来防止位置关注到后续位置。这样掩蔽(Mask)，与输出嵌入被一个位置偏移结合，确保对位置$i$的预测只能依赖位置小于$i$的已知输出。

3.2 Attention

An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.

注意力函数可以被描述成映射一个查询($Q$)和一组键值对($K:V$)到一个输出，这里的$Q$,$K$,$V$都是向量。输出是$V$加权求和计算得到的，分配给每个$V$的权重是由查询$Q$和相应的键$K$的一个相似性函数计算得到的。

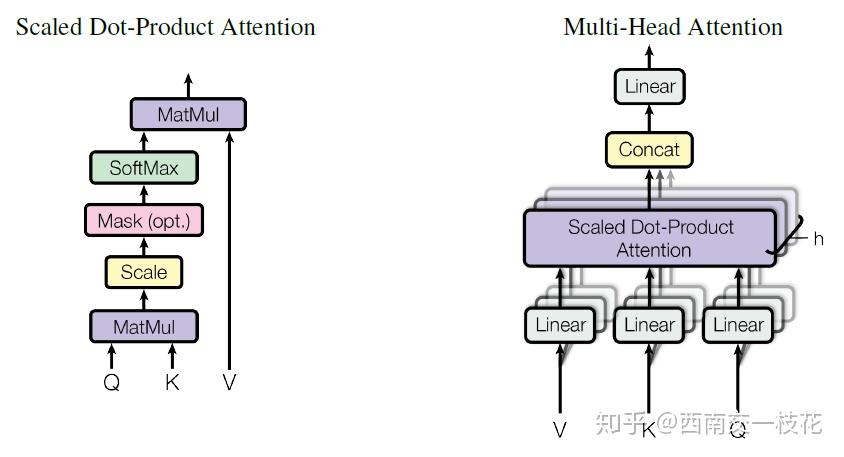
3.2.1 Scaled Dot-Product Attention

We call our particular attention “Scaled Dot-Product Attention” (Figure 2). The input consists of queries and keys of dimension $d_k$ , and values of dimension $d_v$ . We compute the dot products of the query with all keys, divide each by $\sqrt{d_k}$ , and apply a softmax function to obtain the weights on the values.

我们把我们特别的注意力称为“缩放的点积注意力”（图2）。输入是由 $q$和$d_k$ 维的$k$以及$d_v$的$v$构成的。我们计算$q$和所有$k$的点积，每一个除以$\sqrt{d_k}$，然后用一个softmax函数来获得不同$v$的权重。

In practice, we compute the attention function on a set of queries simultaneously, packed together into a matrix $Q$ . The keys and values are also packed together into matrices $K$ and $V$ . We compute the matrix of outputs as:

实际上，我们是把一组$q$打包成一个矩阵$Q$同时计算注意力函数。$k$和$v$也是一起被打包进矩阵$K$和$V$。我们计算输出矩阵如下：

$$
Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}}V)
$$

The two most commonly used attention functions are additive attention, and dot-product (multi-plicative) attention. Dot-product attention is identical to our algorithm, except for the scaling factor of $\frac{1}{\sqrt{d_k}}$. Additive attention computes the compatibility function using a feed-forward network with a single hidden layer. While the two are similar in theoretical complexity, dot-product attention is much faster and more space-efficient in practice, since it can be implemented using highly optimized matrix multiplication code.

两种最常用的注意力函数是加性注意力和乘性(点积)注意力。点积的注意力和我们的算法除了 $\frac{1}{ \sqrt{d_k} }$ 这个缩放因子是一样的。加性注意力用一个单一隐藏层的前馈网络计算相似函数。虽然这两种算法在理论上的复杂性是相似的，但是实践中点积注意力更快，更省空间，因为他可以用高度优化的矩阵乘法代码实现。

While for small values of $d_k$ the two mechanisms perform similarly, additive attention outperforms dot product attention without scaling for larger values of $d_k$. We suspect that for large values of $d_k$ , the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients. To counteract this effect, we scale the dot products by $\frac{1}{\sqrt{d_k}}$ .

然而对于小的$d_k$两种机制表现差不多，对于更大的$d_k$加性注意力优于不带缩放的点积注意力。我们猜想对于大的$d_k$点积变的很大，使softmax进入梯度非常小的区域。为了抵消这种效应，我们把点积缩小了 $\frac{1}{\sqrt{d_k}}$ 。

3.2.2 Multi-Head Attention

Instead of performing a single attention function with $d_{model}$-dimensional keys, values and queries, we found it beneficial to linearly project the queries, keys and values $h$ times with different, learned linear projections to $d_k$ , $d_k$ and $d_v$ dimensions, respectively. On each of these projected versions of queries, keys and values we then perform the attention function in parallel, yielding $d_v$ -dimensional output values. These are concatenated and once again projected, resulting in the final values.

与用$d_{model}$维的$k,v和q$执行单一注意力函数不同，我们发现用分别到$d_k$ , $d_k$ 和 $d_v$不同的学习到的线性映射对线性映射$q,k,v$h次是有益的(结合图片看）。对这些$q,k,v$的每一个投影版我们接着并行地执行注意力函数，生成一些$d_v$维的输出。把这些输出连接起来再次映射生成最终的结果。

Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.

多头注意力让模型共同关注来自不同的在不同位置的子空间特征。用一个注意力头平均抑制了这一点。

$$
MultiHead(Q,K,V) = Concat(head_1 ,…,head_h )W^O
$$
$$
where\ head_i = Attention(QW_i^Q,KW_i^K,VW^V_i)
$$

Where the projections are parameter matrices $W_i^Q\in R^{d_{model}\times d_k}$ , $W_i^K \in R^{d_{model} \times d_k}$ , $W_i^V \in R^{d_{model} \times d_v}$and $W^O \in R^{hd_v \times d_{model}}$ .

In this work we employ $h = 8$ parallel attention layers, or heads. For each of these we use $d_k = d_v = d_{model}/h = 64$ . Due to the reduced dimension of each head, the total computational cost is similar to that of single-head attention with full dimensionality.

在这次工作中我们采用了 $h=8$ 并行注意力层（头）。对这些中的每一个我们用 $d_k = d_v = d_{model}/h = 64$ 。由于减小了每个头的维度，总计算量和单头全维度的注意力相近。

3.2.3 Applications of Attention in our Model

The Transformer uses multi-head attention in three different ways:

Transformer 以三种不同的方式使用多头注意力。

• In “encoder-decoder attention” layers, the queries come from the previous decoder layer, and the memory keys and values come from the output of the encoder. This allows every position in the decoder to attend over all positions in the input sequence. This mimics the typical encoder-decoder attention mechanisms in sequence-to-sequence models.

• 在”encoder-decoder attention”层，查询值来自先前的解码层，存储的键值对来自编码器的输出。这让解码器的每个位置关注输入序列的全部位置。这模仿了在 sequence-to-sequence模型中典型的编解码注意力机制。

• The encoder contains self-attention layers. In a self-attention layer all of the keys, values and queries come from the same place, in this case, the output of the previous layer in the encoder. Each position in the encoder can attend to all positions in the previous layer of the encoder.

• 编码器包含自注意力层。在自注意力层中所有的键值和查询在这种情况下都来自相同的地方——编码器的前层的输出。

• Similarly, self-attention layers in the decoder allow each position in the decoder to attend to all positions in the decoder up to and including that position. We need to prevent leftward information flow in the decoder to preserve the auto-regressive property. We implement this inside of scaled dot-product attention by masking out (setting to −∞ ) all values in the input of the softmax which correspond to illegal connections. See Figure 2.

• 类似的，在解码器的自注意力层让解码器的每个位置关注到解码器的所有位置包括那个位置。我们需要阻止左边的信息流入到解码器来维持自回归的特性。我们通过遮盖（设置为-∞）对应不合理连接的softmax输入的所有值，在缩放点积注意力中实现这一点。

3.3 Position-wise Feed-Forward Networks

In addition to attention sub-layers, each of the layers in our encoder and decoder contains a fully connected feed-forward network, which is applied to each position separately and identically. This consists of two linear transformations with a ReLU activation in between.
$$
FFN(x) = max(0,xW_1 + b_1)W_2 + b_2
$$
While the linear transformations are the same across different positions, they use different parameters from layer to layer. Another way of describing this is as two convolutions with kernel size 1. The dimensionality of input and output is $d_{model} = 512$, and the inner-layer has dimensionality
$d_{ff}$ = 2048.

3.4 Embeddings and Softmax

Similarly to other sequence transduction models, we use learned embeddings to convert the input tokens and output tokens to vectors of dimension $d_{model}$ . We also use the usual learned linear transfor-mation and softmax function to convert the decoder output to predicted next-token probabilities. In our model, we share the same weight matrix between the two embedding layers and the pre-softmax linear transformation, similar to [ 30 ]. In the embedding layers, we multiply those weights by $\sqrt{d_{model}}$ model .

3.5 Positional Encoding

Since our model contains no recurrence and no convolution, in order for the model to make use of the order of the sequence, we must inject some information about the relative or absolute position of the tokens in the sequence. To this end, we add “positional encodings” to the input embeddings at the bottoms of the encoder and decoder stacks. The positional encodings have the same dimension d model as the embeddings, so that the two can be summed. There are many choices of positional encodings, learned and fixed.

In this work, we use sine and cosine functions of different frequencies:
$$
PE(pos,2i) = sin(pos/10000^{2i/d_{model}})
$$
$$
PE(pos,2i+1) = cos(pos/10000^{2i/d_{model}})
$$
where $pos$ is the position and $i$ is the dimension. That is, each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from 2π to 10000·2π . We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset $k$, $PE_{pos}+k$ can be represented as a linear function of $PE_{pos}$ .

We also experimented with using learned positional embeddings instead, and found that the two versions produced nearly identical results (see Table 3 row (E)). We chose the sinusoidal version because it may allow the model to extrapolate to sequence lengths longer than the ones encountered during training.